

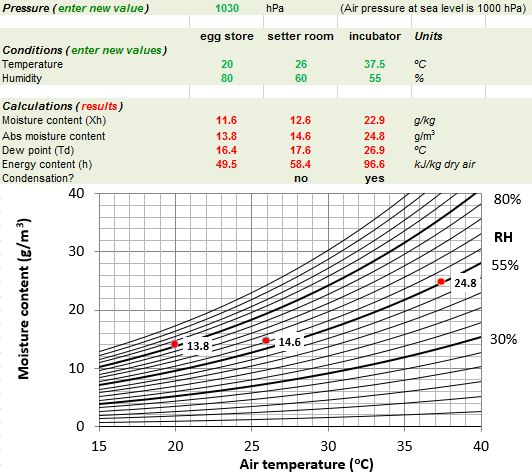
Continuous measurement of internal and external environmental parameters helps us understand how buildings perform. INTRODUCTION The authors of this paper have experienced building performance measurement hands on, first, in situ. Keywords: building measurement, building performance, computer modelling The paper presents various applications of the psychrometric chart for the analysis and reporting of research and discusses the programming of Microsoft Office Excel to generate the chart and display user data. The comfort zone is bounded by lines of constant heat loss from the skin, relative humidity and wet-bulb temperature. As well as results, users would also like to specify and adjust the comfort zone (a shaded area on the chart) for different adaptive or seasonal conditions. Furthermore, many existing charts are complex and cluttered displaying up to ten attributes, being intended for engineering design, whereas presenting the behaviour of living and working environments is focused on wet and dry bulb temperature and relative humidity. It was written because existing programs appear not to cater for the researcher wishing to enter results electronically onto the chart. The psychrometric chart was programmed in Microsoft Office Excel to accommodate measured results. Using the Psychrometric Chart in building measurementsĭeakin University, Geelong, Australia ABSTRACT: This paper centres around the presentation of multiple measured results on a psychrometric chart. relative humidity values.44th Annual Conference of the Architectural Science Association, ANZAScA 2010, Unitec Institute of Technology They can be subsequently added to the plot together with the relevant (vol) and the enthalpy values (h) are displayed (no semicolon) thus Notice in the program that both the specific volume % Plotting the Simplified Psychrometric Chart % Izzi Urieli tpg = dlmread( 't_pg', '\t' ) % saturation temp/pressure t = tpg(:,1) % temperature (C) pg = tpg(:,2) % saturation vapor pressure (kPa) patm = 101.325 % standard atmosphere (kPa) rair = 0.287 % gas constant of air (kJ/kg.K) wg = 622*pg./(patm-pg) % saturation specific humidity plot(t,wg, 'r-' ) hold grid for phi = 0.1:0.1:0.4, % phi = relative humidity 10% - 40% w = 622*phi*pg./(patm-phi*pg) plot(t,w) end for phi = 0.6:0.2:0.8, % phi = 60%, 80% w = 622*phi*pg./(patm-phi*pg) plot(t,w) end % specific volume and enthalpy/wet-bulb-temp tpg1 = dlmread( 't_pg1', '\t' ) t1 = tpg1(:,1) % saturation temperature (C) pg1 = tpg1(:,2) % saturation pressure (kPa) wg1 = 622*pg1./(patm-pg1) % saturation specific humidity % specific volume of dry air (cubic m/kg dry air) (green) vol = rair.*(t1+273)./(patm-pg1) % specific vol at saturation tv0 = patm*vol/rair-273 % air temperature at zero humidity for i = 1:7, plot(, 'g-' ) end % wet bulb temperature (also enthalpy) lines (red) h = t1 + 2.5*wg1 % enthalpy (kJ/kg-dry-air) (displayed) t0 = h % temperature at zero humidity for enthalpy h for i = 1:6, plot(, 'r-' ) end % enthalpy axis and enthalpy lines (black) for h = 10:10:110, % enthalpy (kJ/kg-dry-air) t0 = h % temperature at zero humidity t1 = (h - 12.5)/3.5 % temperature on the enthalpy axis w1 = t1 + 5 % specific humidity on the enthalpy axis plot(, 'k-' ) end plot(, 'k-' ) % the oblique enthalpy axis axis() % limit the range of the chart title( 'Simplified Psychrometric Chart' ) xlabel( 'Dry Bulb Temperature (deg C)' ) ylabel( 'Specific Humidity (gm vap/kg dry air)' ) The suffix g represents the saturated vapor state (following theĬonvention used in steam tables). Humidity, humidity ratio), h represents enthalpy (kJ/kg dry air) and
Represents specific humidity (aka: absolute Thus t represents temperature, p represents The convention in programming that all variable names begin with Thus the enthalpy lines can be plotted parallel to,īut independant of the wet bulb temperature lines. In the enthalpy equation (above) leads to the intercept of theĮnthalpy line with the enthalpy axis as follows: h = T + 2.5 (T + 5) or finally: T = (h - 12.5)/3.5 Notice in the psychrometric chart that the oblique The program: specific humidity: (sometimes known as: The following four equations (refer back to Part Over 5☌ intervals for plotting the wet-bulb temperature andĮnthalpy lines. Over 1☌ intervals for plotting the saturation and constant relative Saturation temperature/pressure data, file t_pg Data is read from 2 datafiles containing water (shown below) is used to plot the Simplified Psychrometric Chart MATLAB program for plotting a Simplified Psychrometric Chart (Updated 3/7/08) MATLAB program for plotting a Simplified


 0 kommentar(er)
0 kommentar(er)
